Изобретение рычага

Неизвестно, с какими бы трудностями столкнулись физики в своих попытках утвердить «золотое правило» механики в его современном виде, если бы задолго до того это правило не было сформулировано в применении к частному случаю. Свыше 2200 лет назад наука открыла закон рычага — простой машины, наглядно иллюстрирующей справедливость «золотого правила». Парадоксально, но рычаг изобрели задолго до того, как был открыт физический закон, объясняющий принцип действия этого устройства.

Принцип работы рычага настолько прост, что это нехитрое устройство впервые стали применять, видимо, еще доисторические люди. Они использовали палки для перемещения больших камней, особенно при воздвижении своих культовых мегалитических сооружений — менгиров, дольменов, кромлехов. В дальнейшем рычажные устройства, сконструированные по гораздо более сложной схеме, стали применяться строителями древнейших городов.

Поскольку самый первый город Иерихон был заложен свыше 10 тыс. лет назад, то можно утверждать, что начиная с этой даты применение рычагов становится все более частым. Регулярно рычажные механизмы применялись в Древнем Египте, где имело место широкомасштабное планомерное строительство разнообразных архитектурных комплексов, объектов хозяйственного назначения и т. п. Каждый в первую очередь представляет себе царские гробницы — пирамиды. Если соблюдать точность, то знаменитые египетские пирамиды представляют собой колоссальные надгробия из каменных блоков.

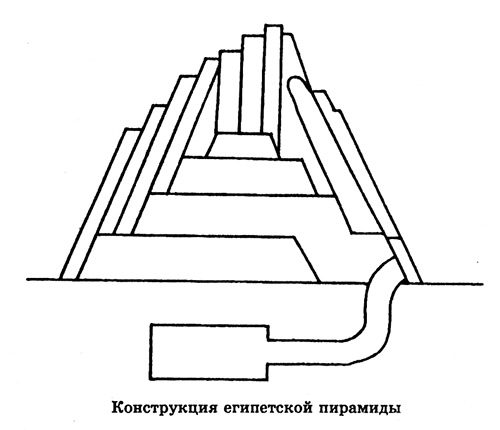
Сама гробница является крупным помещением, уходящим глубоко под землю и заканчивающимся комнатой-усыпальницей, в которой помещался саркофаг с мумией усопшего владыки. Первоначально надгробиями для подземных гробниц фараонов служили огромные плоские мастабы. Лишь фараон Джосер около 4700 лет назад ввел традицию увеличивать мастабы ввысь и превращать их в пирамидальные сооружения. Во время воздвижения пирамид широко применялись рычаги, которые являлись самым необходимым строительным приспособлением, поскольку лишь с помощью подобных устройств было возможно поднимать массивные каменные глыбы на большую высоту.

Затем машины, действие которых основано на принципе рычага, стали использоваться в строительстве повсеместно. Естественно, особое значение они получили в Древней Элладе, т. к. греки уважали архитектуру. Эта наука в их представлении была связана с одной из «идеальных» наук — геометрией. Конструирование механических устройств не было, однако, столь почетным делом. По этой причине рычагом пользовались, не пытаясь объяснить его свойств.

Некоторые древнегреческие мыслители предпринимали попытки разгадать тайны рычага, но все эти начинания оказались тщетны по той причине, что древние подходили к проблеме с предвзятым суждением о свойствах этого простого устройства. Вскоре рычаг был объявлен магическим инструментом, потому что его работа основывалась на полумистических свойствах круга. Дело в том, что концы плеч рычага описывают в пространстве во время своего движения дуги окружностей. А круг и окружность почитались в Древнем мире как священные и волшебные фигуры, ведь по кругу двигались небесные светила.

Круг был «идеален» во всех отношениях, а потому ссылкой на него легко можно было объяснить все самое непонятное в природе и жизни людей. Закон рычага предстояло открыть великому древнегреческому геометру III в. до н. э. Архимеду, жившему в городе Сиракузы на Сицилии. Архимед первым приподнял завесу тайны над магическим кругом, обнаружив число «пи», и поэтому относился к геометрии без излишней предвзятости и идеализации.

Кроме того, Архимед обладал чрезвычайно широким кругозором и занимался практически всеми вопросами существовавших в ту эпоху направлений геометрической науки. Архимед работал над правилами построения фигур, развивал теорию геометрии, конструировал осадные и строительные машины, изучал центры равновесия (центры тяжести), рассчитывал планетарии, т. е. глобусы звездного неба. Единственной отраслью современной ему геометрии и механики, в которой ученый себя никак не проявил, было изобретение механических игрушек.

Таковы предпосылки, благодаря которым Архимед первым описал сущность работы рычажного устройства и на этом основании сформулировал закон рычага. Рычагом называется любой жесткий стержень для приподнимания и перемещения тяжестей. Он имеет точку опоры или ось скольжения, позволяющую ему осуществлять передвижку предметов. Участки стержня, к которым приложены противодействующие силы, называются плечами рычага. Длина каждого плеча равна протяженности отрезка стержня между точкой опоры и точкой приложения силы.

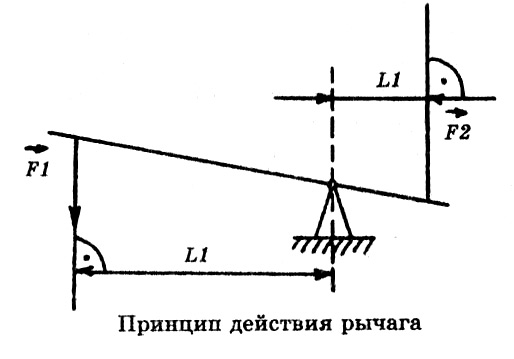
Одной из сил является вес тяжелого тела, которое необходимо переместить. Вторая сила, приложенная к другому плечу, — мускульная. Эту силу развивает человек, работающий с рычагом. Естественно, такая схема сильно упрощена, поскольку рычаги бывают самыми разными, и силы на них действуют также различные. Работа равняется, как и в предыдущих случаях, произведению расстояния на силу. Тело смещается благодаря рычагу в вертикальном направлении.

Однако это расстояние, как несложно убедиться, зависит от длины плеча рычага. Это следует из равенства треугольников, а треугольниками в данном случае являются воображаемые фигуры, отражающие перемещение точек приложения сил и точки опоры. Следовательно, чем ближе к точке опоры вес тяжелого тела и чем дальше приложение мускульной силы, тем больший выигрыш получает человек. Впрочем, понятие выигрыша относительно, т. к. выигрыша в работе рычаг не дает. В этом он схож с любым простым механизмом.

В рассмотренном случае, когда к длинному плечу приложена мускульная сила, происходит выигрыш в силе: малой силой можно уравновесить большую. Но есть рычаг другого рода, который дает выигрыш в расстоянии. В этом случае мускульная сила приложена к короткому плечу. Перемещать слишком тяжелые предметы нельзя, зато свободно передвигаемые таким рычагом тела могут смещаться на большие расстояния. «Золотое правило» механики действует и здесь. Если есть выигрыш в силе, то будет проигрыш в расстоянии, и наоборот.

Многие люди ошибочно полагают, что тела одинакового веса всегда уравновешиваются рычагом. Отнюдь, равновесие между одинаковыми телами наступает лишь в одном случае — когда плечи рычага равны по длине. В остальных случаях равенства не наступает. Это неудивительно. Соотношение сил равняется соотношению длины плеч рычага. То есть при равных силах, когда соотношение равно 1, для установления баланса необходимо, чтобы соотношение длин плеч количественно равнялось той же величине. Единицу в пропорции можно получить при единственном условии: когда длины плеч одинаковы.

В связи с этим любопытна задача о «пустом» рычаге. К нему не приложены никакие внешние силы, кроме тяготения, которое действует на сами плечи простой машины. Плечи равны по длине и изготовлены из одного материала, следовательно, рычаг находится в равновесном состоянии. Если согнуть одно из плеч, нарушится ли равновесие? Оказывается, да! Поразительно, но перетянет длинное плечо.

Это произойдет по следующей причине. В согнутом плече сместится центр тяжести, он приблизится к точке опоры. В результате само плечо окажется короче, потому что длина плеча представляет собой расстояние между точкой опоры и точкой приложения силы (последняя в нашем случае есть центр тяжести, к которому приложен вес плеча). В другом плече центр тяжести находится по-прежнему далеко от точки опоры. Вес обоих плеч не изменился, значит, смещение центра тяжести приведет к нарушению баланса.

Итак, Архимед, обрадованный своим открытием, горделиво утверждал: «Дайте мне точку опоры, и я переверну мир». Если верить римскому литератору и хроникеру Плутарху, сиракузский изобретатель высказался столь категорично в беседе со своим родственником, царем города Сиракузы Гиероном. Отчетливо понимая, что не существует в природе веса, который невозможно сместить посредством подходящего рычага, Архимед заверял царя, что будь у него (Архимеда) в распоряжении другая земля, он бы поднял нашу.

Впоследствии эту крылатую фразу не раз обыгрывали, но, как правило, всегда неудачно, любители ярких выражений. Однако нас сейчас интересует, был ли прав Архимед. Беспредельны ли возможности рычага? Конечно, его возможности напрямую связаны с материалом стержня, прочностью точки опоры и протяженностью длинного плеча.

Предположим, будто бы у нас имеется подходящий рычаг и точка опоры. Теоретически, если все условия соблюдены, нет ничего более простого, чем сдвинуть планету с земной массой. Земля весит 6 на 10²¹ т. Следовательно, рычаг должен иметь длинное плечо всего в 10²³ раз больше короткого. Одна неприятность ожидает последователей Архимеда: неизбежный проигрыш в расстоянии. Чтобы переместить планету с орбиты на толщину атомного ядра, потребуется, очевидно, преодолеть свыше 100 000 км в мировом пространстве, что равно 0,26 расстояния между Землей и Луной.

Если же нам захочется сдвинуть нашу планету на расстояние, равное поперечнику мельчайшей песчинки (10^-6 м), то длинное плечо рычага опишет во Вселенной еще большую дугу — порядка 10¹⁴ км, или 10,6 св. года. Это приближенно равняется расстоянию между Землей и карликовой звездой Росс 154 (10,3 св. года). Бедный Архимед, воспользуйся он современными ракетами, преодолел бы это чудовищное расстояние только много более чем за 1,1 млн лет! Поэтому правота дерзкого утверждения Архимеда относительна.